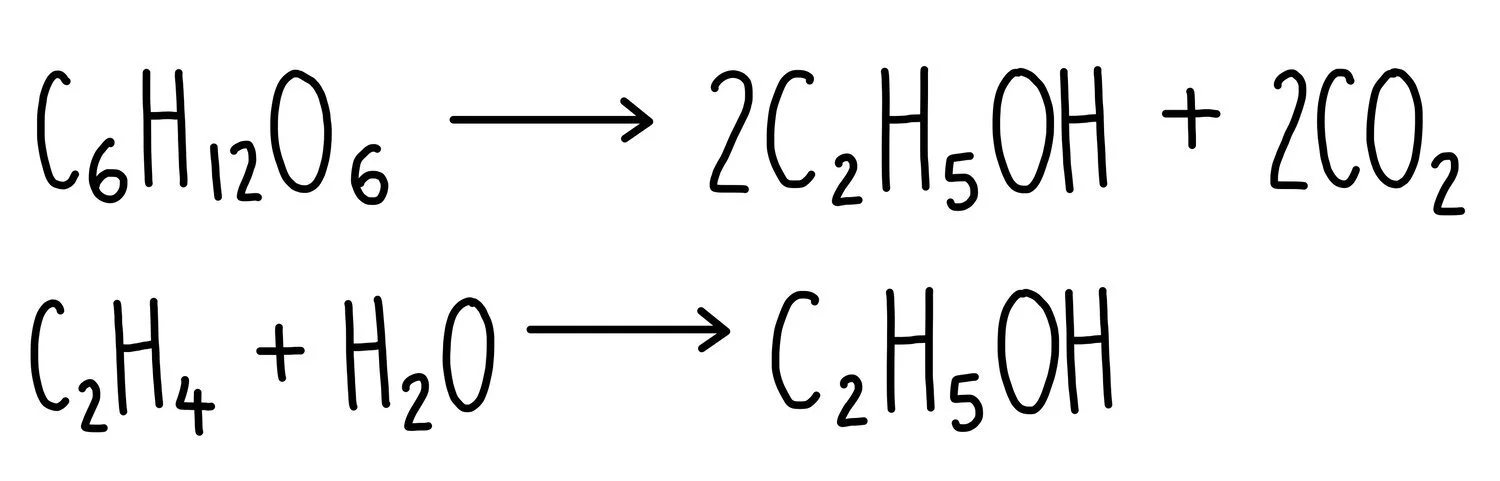Chemical formulae, equations and calculations
Chemical equations use an element’s symbol, rather than writing out its full name. On this page we’ll learn how to write symbol equations as well as how to calculate the number of moles of a substance.
Writing word and symbol equations
Chemical equations can be written using either words or chemical symbols. With chemical equations, we often indicate the state symbols after each molecule or element in the symbol equations to indicate whether they are in solid, liquid, aqueous or gaseous form. For example, a displacement reaction between copper sulfate and magnesium, can be shown as follows:
Writing formulae of compounds
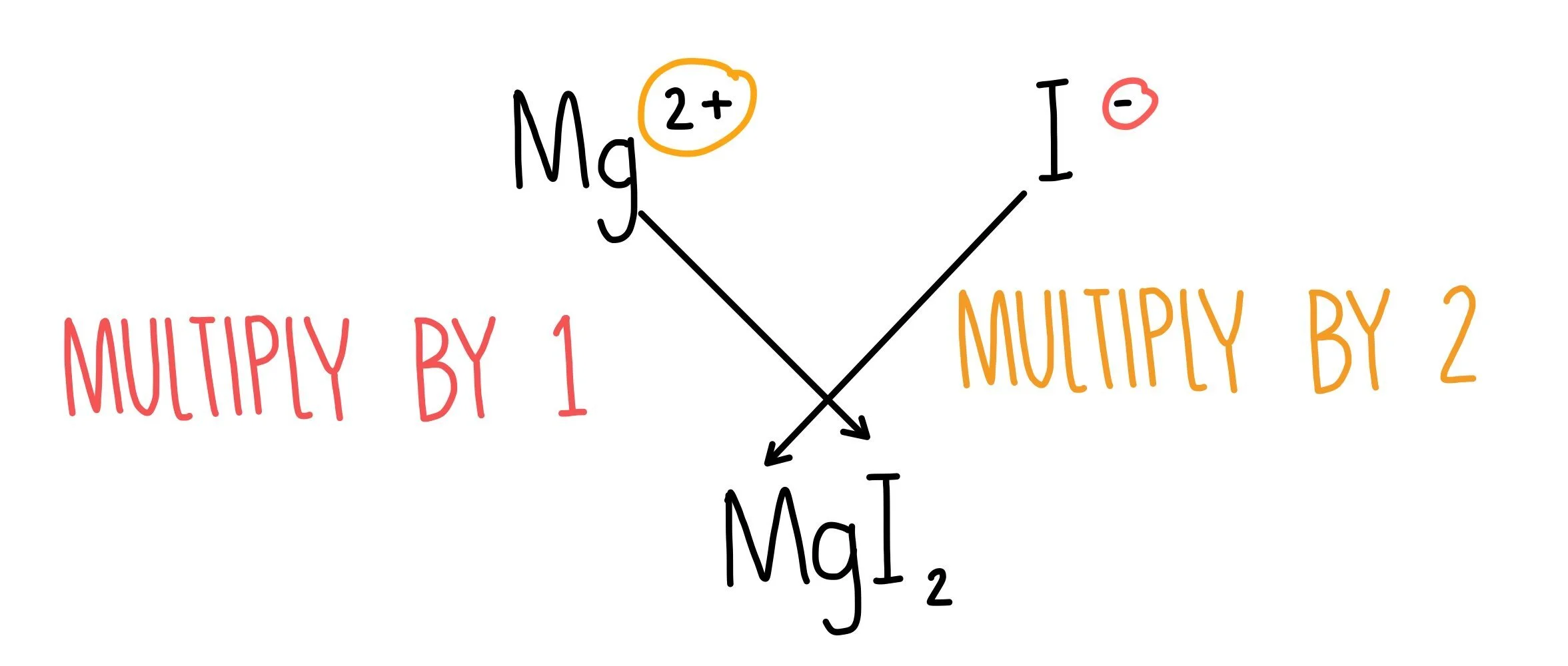
Let’s have a look at how to write the formula of the compound magnesium iodide.
Method:
- Write the formula of magnesium iodide by looking up their symbols on the periodic table. Magnesium is Mg and iodine is I. 1
To work out how many atoms of each element form a compound, look at the charges that would form on each element. Magnesium forms an ion with a +2 charge, since it needs to lose 2 outer electrons to get a full outer shell. Iodide ions have a +1 charge, since iodine needs to gain 1 more electron to get a full outer shell.
For the whole molecule to be unbalanced, we need two iodide ions to balance out the +2 charge on the magnesium ion. This gives us a formula of MgI2.
You can also use the crossing-over method to work out the formula of a molecule if you know the charges of the ions.
Relative formula masses
The relative atomic mass of an element describes how heavy an element is compared to the mass of an atom of carbon-12. You can find the relative atomic mass (RAM) by looking up the element’s mass number on the periodic table. When we do this, we see that calcium has a mass number of 40, which means its relative atomic mass is also 40.
When different elements bond to form a compound, this will have a relative formula mass which is the relative atomic masses of the elements in that compound added together.
Worked example: calculating relative formula mass
Determine the relative formula mass of calcium carbonate, CaCO3
- First work out the relative atomic masses of each element by looking up their mass numbers in the periodic table. Ca = 40, C = 12 and O = 16.
- Add these together. Don't forget to multiply any small numbers by the RAM. From the formula, there is a small 3 written after the oxygen, which means we have three atoms of oxygen in the compound.
- Relative formula mass = 40 + 12 + (16 x 3) = 100
Not that kind of mole..
Moles
A ‘mole’ simply refers to the amount of a certain substance. Just like asking your butcher for a pound of bacon, one mole of an element refers to a particular amount of that element. It is equivalent to 6.02 x 1023 atoms, which chemists like to refer to as Avagadro's number, funnily enough because a guy called Amedeo Avogadro came up with it.
One mole of any element will always weigh the same as its mass number (or RAM). This means that one mole of carbon will weigh 12 g and one mole of calcium will weigh 40 g.
The same thing is true for molecules. Let’s say we have exactly one mole of carbon dioxide gas, CO2. We can determine how much this weighs by working out the relative formula mass (12 + (16 x 2) = 44). So one mole of CO2 weighs 44 g.
Moles, mass and formula mass
We can calculate how many moles of a substance we have by dividing the mass in grams of a substance by molar mass (Mr). Mr is the exact same thing as the relative formula mass.
Worked example: calculating moles from mass and Mr
How many moles are there in 4 grams of sodium hydroxide (NaOH)?
Use the equation moles = mass / Mr
Work out the Mr (formula mass) by adding together the relative atomic masses (the mass numbers). Na = 23, O = 16 and H = 1 so NaOH = 40
Moles = 4 / 40 = 0.1 mol
Percentage yield
Percentage yield describes how much reactant was successfully converted into product. In reality, percentage yield will always be less than 100% due to a handful of reasons. Firstly, some reactant or product will be lost when transferring between containers or filtering, for example. Secondly, the reaction may be incomplete, with not all reactant converted into product. Finally, some reactant may have reacted with a different substance, such as oxygen in the air, to produce something other than the desired product.
Percentage yield is calculated using the following equation:
Worked example: percentage yield
In a school laboratory experiment, a teacher combines sulfuric acid with magnesium to produce 6.25 g of magnesium sulfate. If the maximum yield is 8.5 g, calculate the percentage yield in this experiment.
Percentage yield = (actual yield / theoretical yield) x 100
Percentage yield = (6.25 / 8.5) x 100
Percentage yield = 73.5 %
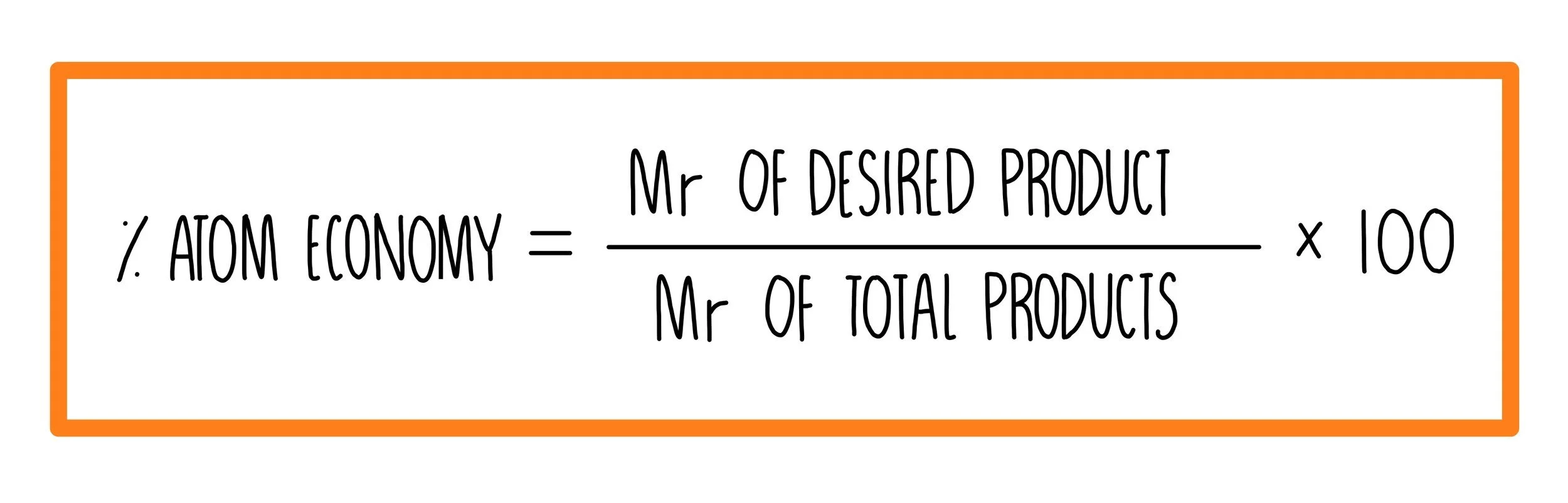
Atom Economy
The atom economy of a reaction is a measure of the amount of reactants which are converted into useful products. The fewer waste products there are, the higher the atom economy. It is cheaper and more sustainable to use reactions with a higher atom economy. The percentage atom economy of a reaction is calculated using the formula:
Worked example:
Ethanol can be manufactured by fermentation of glucose in the presence of yeast. It can also be made through the hydration of ethene. Equations for both reactions are given below:
Calculate the atom economy for each of these reactions.
For the fermentation of glucose:
Mr of desired product (ethanol) = 92
Mr of total products = 92 + 88 = 180
(Mr of desired product / Mr of total product) x 100 = 51%
For the hydration of ethene, ethanol is the only product formed which means that the atom economy is 100% (i.e. all of the reactants are converted into useful product).
Empirical formula and molecular formula
The molecular formula is the actual number of atoms of each element in a compound. The empirical formula is the simplest whole number ratio of atoms of each element in a compound. For example, a molecule of butane has a molecular formula of C4H10. To convert this into a smaller ratio, we can divide each number by 2. This gives us an empiricial formula of C2H5.
You may get a question where you're expected to work out the empirical formula when provided with masses. Look at the worked example below for the steps to do this.
Worked example: calculating empirical formula from masses
A perfume contains a solvents and a mixture of fragrances. A sample of the solvent used in one perfume contains 0.6 g of carbon, 0.15 g of hydrogen and 0.4 g of oxygen. Calculate the empirical formula of the compound used in the solvent.
Step 1: Find the moles of each element using the equation moles = mass / Mr.
- Carbon = 0.6 / 12 = 0.05 mol
- Hydrogen = 0.15 / 1 = 0.15 mol
- Oxygen = 0.4 / 16 = 0.025 mol
Step 2: divide each of the moles by the smallest number calculated. Here, the smallest number of moles is that of oxygen, with 0.025.
- Carbon = 0.05 / 0.025 = 2
- Hydrogen = 0.15 / 0.025 = 6
- Oxygen = 0.025 / 0.025 = 1
Step 3: write out the empirical formula using the ratio calculated. Here we can see that for every atom of oxygen there are two atoms of carbon and six atoms of oxygen. We write this as C2H6O.
Moles, concentration and volume
We can calculate the moles of a solution when we know the concentration and volume. The equation to use is:
The important thing to remember when using this equation is that volume will usually be given in cm3 while concentration is always measured in mol dm-3. Before we can calculate moles, we need to convert volume in cm3 to dm3 by dividing by 1000.
Worked example: calculating moles of a solution
Calculate the moles of sodium chloride in a 100 cm3 solution which has a concentration of 0.5 mol dm-3.
- Convert cm3 to dm3 by dividing by 1000.
- 100 / 1000 = 0.1 dm3
- Calculate moles using the equation: moles = concentration x volume
- Moles = 0.5 x 0.1 = 0.05 mol
Molar volume of a gas
One mole of a gas always takes up the same volume at room temperature and pressure. That volume is 24 dm3 or 24,000 cm3. So if we have one mole of nitrogen gas, we know that it will take up 24,000 cm3 of volume. If we have 2 moles of nitrogen gas, will will have double that volume (24,000 x 2 = 48,000 cm3) and if we have 5 moles it will occupy five times the volume (5 x 24,000 = 120,000 cm3).
This can be summarised in the equation:
Worked example: molar volume of a gas
What volume does 0.6 moles of ammonia gas occupy at room temperature and pressure?
- Use the equation: volume = moles x 24,000 cm 3
- Volume = 0.6 x 24,000
- Volume = 14,400 cm 3 or 14.4 dm 3
Calculate the volume of 7.52 g of ammonia (NH3) gas at room temperature and pressure.
- Moles = mass / Mr
- 7.52 / 17 = 0.44 mol
- Volume = moles x 24
- 0.44 x 24 = 10.56 dm3