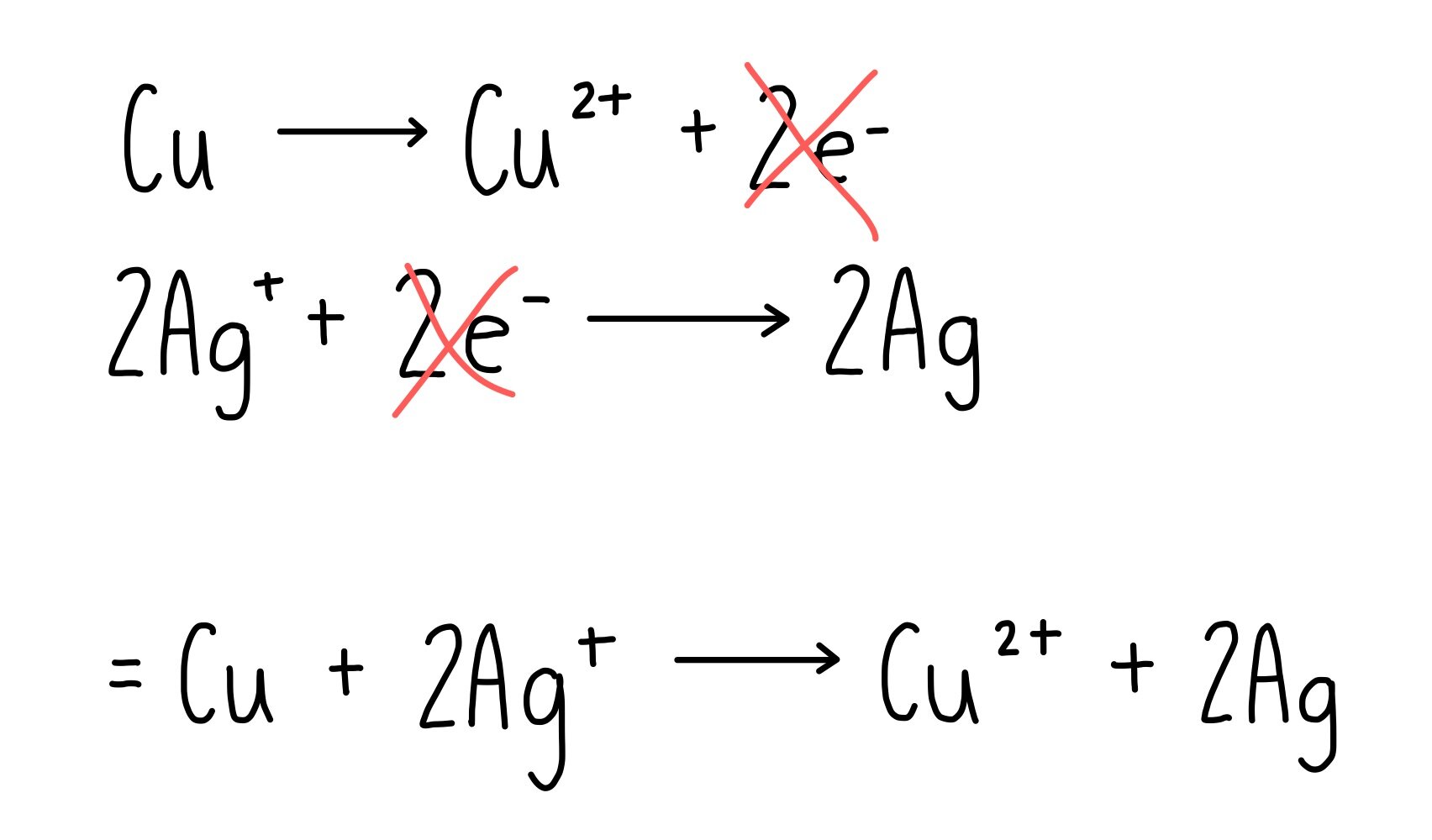Redox and Electrode Potentials
Redox
A redox reaction is a reaction where reduction and oxidation take place — oxidation is the loss of electrons whereas reduction is the gain of electrons.
The thing being oxidised is known as the reducing agent because it transfers electrons to the thing that is being reduced. Likewise, the thing being reduced is known as the oxidising agent, because it transfers electrons to the thing that is being oxidised.
When aluminium and oxygen react to form aluminium oxide, aluminium loses electrons to form Al3+ while oxygen gains electrons to form O2-. Therefore aluminium is oxidised (and acts as a reducing agent) while oxygen is reduced (and acts as an oxidising agent).
Redox reactions can be shown as two half equations – one half equation for the oxidation reaction and the other half equation for the reduction reaction. In the reaction between aluminium and oxygen, our two half equations would be:
You may be given two half equations and be expected to come up with the full redox equation. All you have to do is balance the electrons by multiplying up, cancel out the electrons then add the two half equations together.
Let’s say we have two half equations that show the reduction of copper and the oxidation of silver.
To balance the electrons, we multiply the silver half equation by two. Now we can cancel out the electrons.
Writing more complicated redox equations
You need to know how to balance more complicated half equations, where other species such as H+ and water are present. If you stick to the rules below, you can’t go wrong.
Ensure all the elements (apart from oxygen and hydrogen) are balanced
Balance oxygen by adding water molecules
Balance hydrogen by adding hydrogen ions
Balance the charges by adding electrons – you can check you’ve done this correctly by looking at the oxidation numbers
Worked example – writing half equations
Dichromate ions, Cr2O72-, react with iron (II), Fe2+ ions, in a redox reaction where Cr2O72- is reduced to form Cr3+ and Fe2+ is oxidised to Fe3+. Write the equation for this redox reaction.
We start by writing our two half equations. The iron (II) to iron (III) reaction is pretty straight-forward:
The dichromate one is a little more complicated and we need to follow the rules outlined above.
So far we know that dichromate is converted into chromium (III) ions:
We’re going to start by making sure everything other than hydrogen and oxygen are balanced. In this case, that’s just chromium.
Now we balance the oxygens by adding water molecules. I have 7 oxygens on the left so need 7 lots of water on the right.
Then balance the hydrogens by adding hydrogen ions. I have 14 hydrogens on the right so need to add 14 hydrogen ions on the right.
Then balance the charges by adding electrons. I have a charge of +12 on the left and +6 on the right so I need to add 6 electrons (6x negative charges) to get both sides equal.
Done! If you look at the oxidation numbers of chromium, we can see that we’ve added the correct number of electrons.
- Cr in Cr2O72- = +6
- Cr in Cr3+ = +3
Three electrons are gained by Cr to be converted from dichromate to chromium (III) ions. Because there are 2x Cr, that is a total of 6 electrons gained.
The last step is to put these two half equations together by balancing the electrons, cancelling out and merging together.
As well as cancelling out electrons, you may also have to cancel any protons or water molecules if they are on opposite sides of the two half equations. In this case, it wasn’t necessary but it is worth bearing in mind.
Redox titrations
Acid-base titrations are used to work out the volume of acid needed to neutralise a base (or vice versa) to work out its concentration. Redox titrations are basically the same thing except it’s used to work out the volume of oxidising agent needed to react with a reducing agent (or vice versa) and from the volume, we can work out its concentration. It’s the same set-up as acid-base titrations except indicator dyes aren’t used.
Transition metals are used as the oxidising or reducing agent because they can exist in multiple oxidation states – so they are good at being oxidised or reduced. They also change colour when they gain or lose electrons, which tells us when the reaction is complete.
Here’s the method for carrying out a redox titration:
- Measure a certain volume or the reducing agent (e.g. Fe2+ solution) using a pipette and transfer to a conical flask
- Add an excess of dilute sulfuric acid to the conical flask.
- Add a solution of oxidising agent (e.g. MnO4-) to a burette. Record the initial volume.
- Open the tap, slowly adding the oxidising agent to the conical flask. Swirl to mix.
- When the solution changes colour, close the tap on the burette and record the final volume. Placing a white tile underneath the conical flask makes this easier to spot.
- Calculate the titre volume (initial volume – final volume).
- Repeat to get concordant titres and calculate a mean.
- Remember that this can be carried out the other way – with the oxidising agent in the conical flask and the reducing agent in the burette.
Worked example – redox titration calculations
Ethanedioic acid, (COOH)2, is present in rhubarb leaves. A student carries out a redox titration using aqueous cerium(IV) sulfate, Ce(SO4)2 (aq), to determine the percentage, by mass, of ethanedioic acid in rhubarb leaves.
In the titration, Ce4+ (aq) ions oxidise ethanedioic acid in hot acid conditions:
Ce4+(aq) ions have a yellow colour. Ce3+(aq) ions are colourless.
The student weighs 82.68 g of rhubarb leaves and extracts ethanedioic acid from the leaves. The ethanedioic acid is added to dilute sulfuric acid to form a colourless solution which is made up to 250.0 cm3 with distilled water. The student heats 25.00 cm3 of this solution to 70°C and titrates this volume with 0.0500 moldm–3 Ce(SO4)2 from the burette. The student repeats the titration to obtain concordant (consistent) titres.
- Titration 1 = 23.25 cm3
- Titration 2 = 23.50 cm3
- Titration 3 = 23.15 cm3
Calculate the percentage, by mass, of ethanedioic acid in the rhubarb leaves.
- Only titrations 1 and 3 are concordant so we discard titration 2 before calculating a mean. Concordant titres are within 0.1 cm3 of each other.
- Mean titre = 23.20 cm3
- Moles = volume in dm3 x concentration
- Moles of Ce4+ = (23.20/1000) x 0.05 = 1.16 x 10-3
- There is a 2:1 ratio between Ce4+ and (COOH)2
- Moles of (COOH)2 in 25 cm3 = 1.16 x 10-3 / 2 = 5.8 x 10-4
- Moles of (COOH)2 in 250 cm3 = 5.8 x 10-4 x 10 = 5.8 x 10-3
- Mass = moles x Mr
Mass of ethanedioic acid = 5.8 x 10-3 x 90 = 0.522
Percentage mass in rhubarb = 0.522 / 82.68 x 100 = 0.631 %
Iodine-thiosulfate titrations
Iodine-sodium thiosulfate titrations are a type of titration that can be used to work out the concentration of an oxidising agent. To carry out an iodine-sodium thiosulfate titration, carry out the procedure below:
Use a measuring cylinder to measure out a certain volume (e.g. 25 cm3) of oxidising agent e.g. potassium iodate (V) solution, KIO3.
Add this to a beaker containing an excess of acidified potassium iodide solution, KI. The iodate ions (IO3-) will oxidise the iodide ions to iodine.
Add a solution of sodium thiosulfate, Na2S2O3, of known concentration to a burette.
Transfer the iodine solution to a conical flask and slowly add the thiosulfate from the burette into the conical flask.
When the iodine turns pale yellow, you are close to the end point. Add starch to the mixture to serve as an indicator. A blue colour tells you that there is still iodine present.
Keep adding the sodium thiosulfate drop by drop until the blue colour disappears. You have reached the end point as all the iodine has reacted.
Record the titre volume for the sodium thiosulfate required for complete oxidation. Use this to calculate the concentration of the iodine solution.
The equation for the titration is:
Worked example – thiosulfate titrations
In an experiment, iodide ions from potassium iodide react with iodate(V) ions and hydrogen ions from hydrochloric acid according to the ionic equation:
The amount of iodine formed can be determined by titration with sodium thiosulfate solution of known concentration. The equation for this reaction is:
30.0 cm3 of a solution of hydrochloric acid was added to an excess of potassium iodate(V) and potassium iodide solutions in a conical flask. The iodine formed in the conical flask was titrated with sodium thiosulfate solution of concentration 0.100 mol dm–3. The mean titre was 45.00 cm3 . Calculate the concentration of hydrochloric acid in mol dm-3.
- Moles of thiosulfate = (45/1000) x 0.1 = 4.5 x 10-3 mol
- There is a 2:1 ratio between thiosulfate : iodine
- Moles of iodine = 4.5 x 10-3 / 2 =2.25 x 10-3 mol
- There is a 3:6 ratio between iodine : hydrogen ions
- Moles of H+ = 4.5 x 10-3
- Concentration of HCl = 4.5 x 10-3 / (30/1000) = 0.15 mol dm-3
Electrochemical cells
Electrochemical cells are cells that use redox reactions to generate electricity. Oxidation happens in one half cell and electrons move through a wire to the other half cell, where reduction takes place.
For example, an electrochemical cell consisting of copper and zinc half cells will work like this:
Zinc is oxidised since it loses electrons more readily than copper. Electrons are lost from zinc which travel through the wire to the copper half cell. The zinc atoms move into solution when they are converted into aqueous ions, so the zinc electrode will lose mass and get smaller.
Copper ions are reduced to form copper atoms. The aqueous ions are converted into solid copper atoms which are deposited on the electrode, so the copper electrode will gain mass and get bigger.
You may be given information on the electrode potential of a half cell. This value tells you how easily a metal is oxidised. The more negative the electrode potential, the more likely the metal is to be oxidised. The more positive, the more likely it is to be reduced. Here are the electrode potentials for the zinc and copper half cells:
Zinc has the more negative electrode potential so we know it is more likely to be oxidised. We need to reverse the direction of the arrow for the reduction reaction, to show that the reverse reaction is taking place.
When drawing half-cells, it’s the rule that the half-cell with the more negative electrode potential (the oxidised half-cell) goes on the left.
The potential of the whole cell is calculated by subtracting the more negative (oxidised) potential from the more positive (reduction) potential. In other words, the electrode potential from the right-hand side half-cell minus the electrode potential from the left-hand side half-cell.
Using the data for the zinc/copper electrochemical cell given above, the electrode potential would be 0.34 - -0.76 = 1.1. Remember that the cell potential will always be positive because the more negative value is being subtracted from a more positive value.
You can also have a half cell made up of the same element in two different oxidation states e.g. Fe2+ / Fe3+. In this case, a platinum electrode is used. Some electrochemical cells involve gases, which are bubbled over a platinum electrode in a solution of its aqueous ions.
The standard electrode potential is the electrode potential of a half cell when measured against a standard hydrogen electrode. The official definition is:
- Standard electrode potential = the voltage of a half-cell when connected to a standard hydrogen electrode and measured under standard conditions (1 mol dm-3 concentrations, 298 K and 100 kPa).
It is important to measure electrode potentials at standard conditions, as variations in temperature, pressure and concentration can affect the position of equilibrium of the redox reactions, therefore changing the cell potential.
The electrochemical series
We’ve already seen that the more negative the electrode potential, the more readily a metal will lose electrons to form positive metal ions. This means that a half cell with a more negative potential is more reactive than one with a less negative potential.
For non-metals, which gain electrons when they react to form negative ions, the more positive the electrode potential the more likely they are to gain electrons and become reduced. This means that a non-metal half-cell with a more positive potential is more reactive than one with a less positive potential.
Just like the reactivity series, standard electrode potentials can be placed in order from the most negative to the most positive – this is called the electrochemical series. The half-reactions at the top of the series show the half cells that are most likely to be reduced and the ones at the bottom show the half cells that are most likely to be oxidised.
You can use the electrochemical series to work out whether a reaction will happen. For instance, whether magnesium will react with iron (III) ions, Fe3+. If we pick out the electrode potentials for the two relevant half equations, we can see that magnesium has the more negative value, so it will lose electrons and the reaction will occur in the backwards direction.
The iron half equation has a more positive value so it will occur in the forwards direction, with Fe3+ being reduced into Fe2+.
Putting those two half equations gives us:
We can see that the reaction will take place.
Now let’s see whether hydrogen ions (i.e. an acid solution) will react with solid copper. The hydrogen half equation is the most negative, so we need to rewrite it in the backwards direction.
The copper half equation is more positive so it is written in the forward direction.
Cancelling out the electrons and putting these two half equations together gives us:
This tells us that copper won’t react with hydrogen ions – it’s the copper ions which react with hydrogen gas.
That’s not to say that certain reactions will never happen, only that they won’t happen under standard conditions. If you change the concentration, pressure or temperature, this will shift the position of equilibrium in the reversible reaction and change the value of the electrode potential, meaning that certain reactions that won’t occur at standard conditions may be possible once the conditions have changed.
Even reactions which are possible according to their electrode potentials may not happen in reality due to a high activation energy or an extremely slow reaction rate.
Storage and fuel cells
Electrochemical cells are used in batteries, also known as energy storage cells, using the electrons released in redox reactions to generate electricity. You might be given two half-equations that are occurring in an energy storage cell and be asked to write the overall reaction and calculate the voltage of the battery. You’d do this in the same way as we saw for other electrochemical cells, as shown below.
For example, suppose we have a nickel/cadmium battery and are given the following half-equations:
The first thing we do is identify the half-cell with the more negative potential and reverse the equation.
Then multiply the equations if necessary so that the electrons are equal.
Now cancel out anything that is the same and put the equations together.
To calculate the cell voltage, we use the formula: cell voltage = reduction reaction – oxidation reaction, or more positive potential – more negative potential.
For the nickel/cadmium battery, this is 0.52 - -0.88 = 1.4 V. Remember that the overall cell voltage will always be positive.
A fuel cell is a bit different to an energy storage cell – it produces electricity by reacting fuel with an oxidant. In hydrogen fuel cells, hydrogen is reacted with oxygen.
Hydrogen is oxidised at the anode. It loses electrons to form hydrogen ions.
The anode and cathode are separated by a polymer electrolyte membrane (PEM) which is only permeable to the hydrogen ions. The electrons have to move around the circuit in the opposite direction.
The movement of electrons around the circuit towards the cathode generates an electric current.
At the cathode, oxygen gains electrons (it is reduced) and combines with hydrogen ions to produce water.
One advantage of hydrogen fuel cells is that they only form water as a waste product — they don’t generate any polluting gases. Electrochemical cells are also more efficient than combustion engines because energy is not wasted as heat. However, toxic chemicals are used which need to be carefully disposed of once batteries have run out and these chemicals are highly flammable, posing a fire risk.